Aerodynamics and air-resistance

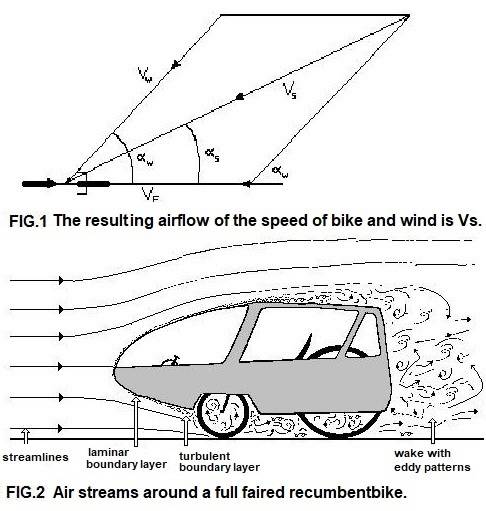
The air speeds of wind and bike, are vector units that should be added up according FIG.1. The flow velocity of the air along the cyclist is Vs: the result of wind speed and wind direction (Vw) + speed and direction of the cyclist (Vf). In case of a small and slow object, the air flow can easily close again behind it; such a flow pattern is called laminar. Turbulence may occur at higher speeds. This results in a wake behind the object with negative pressure and eddies; it takes extra energy, that must be overcome (see FIG. 2).

There are two types of aerodynamic resistance: 1. Friction of the air molecules 2. Energy loss by eddies and underpressure  in the wake.

The change of the air velocity at the surface in the laminar boundary layer is evenly. The thin layers of air are moving over each other. If the object is small and sleek, and the boundary layer laminar, there will be almost no wake. Further downstream the boundary layer is getting thicker, because the friction at the surface keeps slowing the air. Here comes a tipping point, where the boundary layer gets turbulent. Factors like roughness of the surface and the degree turbulence of the approaching air, play a role. Then the turbulent boundary layer leaves the object and creates a distorted flow field behind it: the wake. The energy in the eddies can increase the resistance by a factor of 3 to 10.

Larger bodies and/ or rough surfaces give a wider wake. Eddies and turbulence can absorb a lot of energy and thus induce a large resistance. For some objects and speeds it can be beneficial to keep the laminar layers very thin. This is done by making the boundary layer turbulent very quickly. The air flow goes around the body + the turbulent boundary layer and builds up no, increasingly thick, laminar layers. The air flow comes off the body in later stage, and this results in a smaller wake. The frictional resistance of these rougher surfaces is higher, but the total resistance is lower, because air layers are thinner and the wake remains small.

This is the secret of the dimples in the golfball and the rougher surface of some time-trial suits (see FIG. 3).

The drag coefficient (Cd-value) of a cylinder changes with the Reynold's number. If the surface is rough, the friction and so the Cd-value is a bit higher. However, the quickly turbulent boundary layer results in a smaller width of the wake and creates less losses. The rougher the surface, the sooner this happens. Here it happens at 50.000. The value of the smooth cylinder  drops later at 500.000, but it will be lower! So if the Reynoldsnumber is in the 1.000.000 range, you must choose a smooth cylinder. Although the Reynold's number is important for the understanding of aerodynamic phenomena, it is not of much practical use.

    The most important factor in our calculations is the "form factor" or Cd-value (friction = drag). This includes actually the above theoretical stories expressed in a practical rating . We can not calculate the Cd-value exactly in advance, but we use existing data from aerodynamic investigations or computer based models. We can often make an educated guess, and do a number of measurements, for example on a windless day at a known slope + distance. If the calculated speed matches the actual speed, we have found the Cd-value. This is not a real constant value and can vary somewhat over a speed range (see fig. 3). The Cd for a clunkerbike is 1,1; for a deep seated rider 0,9 or even 0,8 for low recumbents. The real leap forward is shown in streamlined recumbents: Alleweder 0,45; Quest 0,22; record vehicles < 0,1

Triathlon and time trial bikes keep improving in the margin; the resistance of the bicycle is roughly one-fourth of the resistance of the cyclist. Where a fairing brings down the Cd-value with tenths, time trial-and triathlon bikes have to do it with percents and promilles. Flattened frames and less spoked wheels are the result. Of course, these are minor improvements of the Cd-value, but there must be some costs (not only in euro). The lateral stiffness of the frame is decreasing; the wheels are heavier and more sensitive to crosswinds. Riding with strange positions like Obree and Boardman did, is profitable, but then again those are banned now. Disk frontwheels are dangerous in crosswinds; they create large lateral forces because of the wing-effect (see FIG. 4 c). A disk rear wheel is in the wake of the seat tube and thus offers much less advantage. For the average rider is a half-height rim with 16 spokes for and 20 at the rear will be a workable compromise for all conditions. For randonneur-or mountain-biking we need more spokes, but the average speeds are lower and the aerodynamics play a smaller role. 

Besides riding time-trials and records there are also aerodynamic phenomena that are important for a group of riders (the peloton). There were a number of experiments in wind tunnels with simple models as cylinders. Of course, we cannot say that aerodynamics are the same as cyclists, but there appears to be a corresponding trend. If the gap between the two cylinders two times the diameter of a cylinder, the front cylinder a resistance reduction of 15% and rear virtually no air resistance. If the distance between cylinders is 3 x the diameter of the cylinder, the advantage for the first is lost, but for second they found an advantage of 75% upto 8 x the diameter of the cylinder .

Practical measurements in the peloton only show savings of ± 30% for the second rider ; still, this is an important reason to ride in a group. Even the first rider saves energy when he's followed close enough. Alternating and saving forces, is the method to use the energy in the group as well as possible. During team time-trials and in the peloton this has always been done! In a group of four men only the first one has to deliver 30% more power; by alternating they invest only 7.5% extra power per person.

In HPV-races for streamlined bikes these tactics are not working! If you put two ideal streamliners behind each other in a wind tunnel, with one length space, it shows the first one has some advantage, but the rear one has a double disadvantage. In practice it might be less than in the experiment, but the conclusion that it makes no sense, is obvious!

The air resistance: R air = 0.5 * ρ*  Cd * A    (ρ the density of air )

The density of air at 1 bar (in Netherlands approximately 1.23 kg/m³; on 1800 m ± 1 kg/m³); v is the velocity of the air flow to the cyclist; (A) is the frontal surface. For a guy from 2 m and 100 kg upright on a clunkerbike A will be 0, 75 m ²; for a deep seated rider 0, 35 m ² (upright 0, 6 m ²), for a low recumbent 0, 25 m ² and an Alleweder velomobile 0, 5 m².  The property of most importance for the streamlined bicycle design, is the factor Cd * A. Riding at higher altitudes will deminish the density ρ and result in higher speeds.

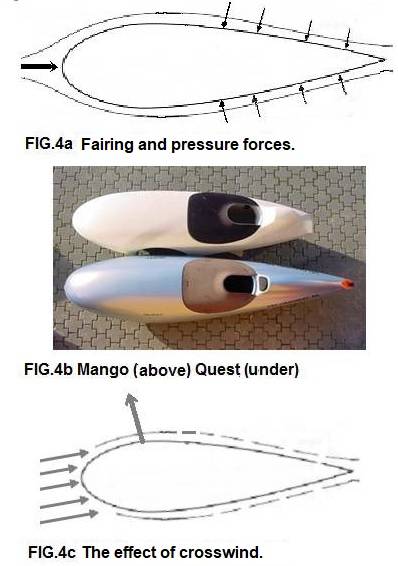
To the front of a streamline creates a pressure force that loss, but the forces on the tip of tail have a small forward component, which is a part of the pressure loss. This is also the function of a tail-cone, which is used on recumbents. The form of this streamlined profiles, is thoroughly studied in aviation engineering (NACA profiles). Ideal is a flattened form of Fig. 4a; This general form, the roundness in front and the pointed tail tip, must be preserved. A streamlined record bike will just full-doing wide to the driver presses. Streamline design is make choices; at record vehicles are the choices largely determined by the laws of aerodynamics. Especially two-wheelers are very cross-wind sensitive, see fig. 4 c. At a small wind angle there will be a resultant force on the lee-side, with a small forward-facing component (sailing effect). The rider will respond by "hanging against the wind " ; any disruption of this balance, by buildings or a passing car, will have a large influence.

That's why most production streamliners are velomobiles; but even the Alleweder is sensitive to turbulence of buildings and passing trucks at wind force 9 ! The frontal area of velomobiles is approximately 0,4 to 0,5 m². The Mango (fig. 4b) has a cut-off tail and open wheel arches, the Cd-value is 0,3; The Quest is "made for speed": no compromise; the Cd-value is 0,22. Cutting off the tail point like in the Mango design, provides limited losses; after the inventor this is called a Kamm-tail.

What does a good fairing look like?

The optimum ratio between the width and length of the profile is about 1: 4 or 1: 5. The maximum width must be on about a third of the length. Make the frontal area as small as possible. Make sure the wheels cause the least possible disturbance, d.w.z. the shape pull the power line as far as possible down through. All the holes in the streamline deteriorate the Cw-value of the vehicle. A tricycle can easily stand still; a two-Wheeler has fittings. Traditional one uses there feet for, through holes or close shutters flapping in the housing; support wheels (see fig. 6b) do not always. A record bicycle may not be practical, because then you don't row records. All the holes in the streamline should be avoided, because they cost energy. The rider cannot stop and start, because the power line close taped:. Even the little hole for breathing closes during the last three hundred meters . The last hundred meters go with ± 35 m per second and are ignored within ten seconds. The shape factor (Cd-value) of these machines is near 0,1; the frontal surface is ± 0.25 m² for a two-wheeler, and 0,40 m² for a tricycle. So you can't ride worldrecords any more with a tricycle .

  Modern carbon rims are wider than the tire to optimise the profile. This means you should not use an extra small or extra wide tire, for Cd-value will be higher!

Record vehicles like the Varna, have a team of helpers; two man at the start that tape the fairing and launch the bike, and two man catch the bike at the end of the race, because the bicycle just falls over. The fairing can be split into two parts,  a left / right part, or a under and upper half (see FIG. 5a and 6a). Attention to fresh air is no luxury; record vehicles can be so  air tight that there is lack of oxygen.

Here we see some of the fastest bikes at the moment (estimated Cd-value < 0,1). Virtual Rush is a radical design. There is no window, but there is a camera in the tail and a small screen mounted inside (estimated Cd is 0.09). Supposedly the Eivie (fig. 7a) is the design with the lowest Cd-value: about 0,07. The rider sits/ lies with his back in the direction of travel and looks through a mirror via a tiny window in front. The frontal area of these designs is around 0, 2 m². Virtual Rush has a tail-plane (extra resistance!); the tip of Eivie also tends to be a tail-plane. It turns out that very good aerodynamics reduce the stability at high speed; a phenomenon that was already known by sports cars and motorized speed records. You might be able to improve that by moving the pressure point of the air behind the center of gravity, but that reduces the lateral stability. To be fairly stable in cross-winds, the pressure point of the air should be in front the center of gravity. Varna scores better in this aspect than Eivie and Virtual Rush, who could draw their noses further down, but that will result in a higher Cd.

The world record in september 2013  was set at 133.78 km/h, by the "Postmen" team of Technical University Delft , with the rider Sebastian Bowier (see FIG. 9), but this has been been improved now!

For making a fairing we use a mold (the plug). Making a good mold is crucial; certainly if this will be used several times. One can choose between a positive and a negative mold. For a as smooth as possible surface of the fairing, it takes a negative mold. The laminate is pasted on the inside of the mold. To prevent adhesion of the laminate to the mold, we use several layers of PVA (polyvinyl alcohol). This is soluble in water. It is common integrate a number of sockets for a water hose in the mold. If the laminate has hardned, we can use water pressure to separate the mold and the fairing. If the fairing, as in the case of the Eivie, is just a shell around a frame, we can use glass fibers. If the fairing is the structure carrying the load, like the Kingcycle Mango, you have to use carbon-epoxy. The Mango two-wheeler was a design with short wheelbase; This turned out to be not so stable and crashed at high speed during a record attempt on Battle Mountain.  

A video of that speedwobble can be seen at  https://www.youtube.com/watch?v=i5Dapy1xUq0

Streamlined trikes are much more stable than streamlined two-wheelers. Surprsingly one of the first recumbent bikes available in Holland, had a full fairing: the Belgian Velerique (FIG.10). This was very spacy; I can't imagine it could be used for commutting in our windy climate.  The frontal area was about 0,6 m² ; the Kingcycle Mango only needs a third of that.

A design of Kingcycle that is often used, is the tent bike. We see a picture of such a bike, the American Lightning F40 in FIG. 11b; a fixed nose cone and tail cone with in between a kind of tent, made of Lycra. It is the dressed-up version of their standard model P38 (FIG. 11a). The F40 is reasonably suitable for everyday use and has had great success in the Race Across AMerica (RAAM). This is a difficult race: with 4 riders 4680 km non-stop (121 hours, 38.7 km/h average)! However, the Cd-value of that bike will not be lower than 0,5 and the frontal area is approximately 0,4 m². A usable full faired bike , that is also at stable in cross-winds, is not easy to design. I would not like to ride the Lightning X-2 from FIG. 11 c in windy weather. Probably combinations of a tailcone and a windshield, like Zzipper or HP Velotechnik Streamer, are a better compromise. Check out http://www.fietsanders.nl/ at Vicap.

Want to know more?

See: http://www.princeton.edu/~asmits/Bicycle_web/bicycle_aero.html or: http://www.analyticcycling.com

Of course, there is information at Sheldon Brown: http://www.sheldonbrown.com/brandt/wind.html or http://sheldonbrown.com/rinard/aero/index.htm

Andreas Fuchs: The trim or aerodymically faired single-track vehicles in crosswinds: http://www.ihpva.org/projects/tools.htm

Wind and aero wheels: http://www.wing-light.de/TechTalk/yaw.htm , and Tony Foale: http://www.tonyfoale.com/Articles/Aerodynamics/AERO.htm

Books/articles: Bicycling Science-D Wilson (with contributions or j. Papadopoulos) third edition 2004 ISBN: 0-262-73154-1